More pypsa features: more complex dispatch problems

More pypsa features: more complex dispatch problems#

Note

If you have not yet set up Python on your computer, you can execute this tutorial in your browser via Google Colab. Click on the rocket in the top right corner and launch “Colab”. If that doesn’t work download the .ipynb file and import it in Google Colab.

Then install the following packages by executing the following command in a Jupyter cell at the top of the notebook.

!pip install pypsa matplotlib cartopy highspy

Note

These optimisation problems are adapted from the Data Science for Energy System Modelling course developed by Fabian Neumann at TU Berlin.

(Repeting) basic components#

Component

Description

Network

Container for all components.

Bus

Node where components attach.

Carrier

Energy carrier or technology (e.g. electricity, hydrogen, gas, coal, oil, biomass, on-/offshore wind, solar). Can track properties such as specific carbon dioxide emissions or nice names and colors for plots.

Load

Energy consumer (e.g. electricity demand).

Generator

Generator (e.g. power plant, wind turbine, PV panel).

Line

Power distribution and transmission lines (overhead and cables).

Link

Links connect two buses with controllable energy flow, direction-control and losses. They can be used to model:

  • HVDC links
  • HVAC lines (neglecting KVL, only net transfer capacities (NTCs))
  • conversion between carriers (e.g. electricity to hydrogen in electrolysis)

StorageUnit

Storage with fixed nominal energy-to-power ratio.

Store

Storage with separately extendable energy capacity.

GlobalConstraint

Constraints affecting many components at once, such as emission limits.

Let’s consider a more general form of an electricity dispatch problem#

For an hourly electricity market dispatch simulation, PyPSA will solve an optimisation problem that looks like this

(3)#\[\begin{equation} \min_{g_{i,s,t}; f_{\ell,t}; g_{i,r,t,\text{charge}}; g_{i,r,t,\text{discharge}}; e_{i,r,t}} \sum_{i,s,t} o_{s} g_{i,s,t} \end{equation}\]

such that

(4)#\[\begin{align} 0 & \leq g_{i,s,t} \leq \hat{g}_{i,s,t} G_{i,s} & \text{generation limits : generator} \\ -F_\ell &\leq f_{\ell,t} \leq F_\ell & \text{transmission limits : line} \\ d_{i,t} &= \sum_s g_{i,s,t} + \sum_r g_{i,r,t,\text{discharge}} - \sum_r g_{i,r,t,\text{charge}} - \sum_\ell K_{i\ell} f_{\ell,t} & \text{nodal energy balance : bus} \\ 0 &=\sum_\ell C_{\ell c} x_\ell f_{\ell,t} & \text{KVL : cycles} \\ 0 & \leq g_{i,r,t,\text{discharge}} \leq G_{i,r,\text{discharge}}& \text{discharge limits : storage unit} \\ 0 & \leq g_{i,r,t,\text{charge}} \leq G_{i,r,\text{charge}} & \text{charge limits : storage unit} \\ 0 & \leq e_{i,r,t} \leq E_{i,r} & \text{energy limits : storage unit} \\ e_{i,r,t} &= \eta^0_{i,r,t} e_{i,r,t-1} + \eta^1_{i,r,t}g_{i,r,t,\text{charge}} - \frac{1}{\eta^2_{i,r,t}} g_{i,r,t,\text{discharge}} & \text{consistency : storage unit} \\ e_{i,r,0} & = e_{i,r,|T|-1} & \text{cyclicity : storage unit} \end{align}\]

Decision variables:

  • \(g_{i,s,t}\) is the generator dispatch at bus \(i\), technology \(s\), time step \(t\),

  • \(f_{\ell,t}\) is the power flow in line \(\ell\),

  • \(g_{i,r,t,\text{dis-/charge}}\) denotes the charge and discharge of storage unit \(r\) at bus \(i\) and time step \(t\),

  • \(e_{i,r,t}\) is the state of charge of storage \(r\) at bus \(i\) and time step \(t\).

Parameters:

  • \(o_{i,s}\) is the marginal generation cost of technology \(s\) at bus \(i\),

  • \(x_\ell\) is the reactance of transmission line \(\ell\),

  • \(K_{i\ell}\) is the incidence matrix,

  • \(C_{\ell c}\) is the cycle matrix,

  • \(G_{i,s}\) is the nominal capacity of the generator of technology \(s\) at bus \(i\),

  • \(F_{\ell}\) is the rating of the transmission line \(\ell\),

  • \(E_{i,r}\) is the energy capacity of storage \(r\) at bus \(i\),

  • \(\eta^{0/1/2}_{i,r,t}\) denote the standing (0), charging (1), and discharging (2) efficiencies.

Note

Per unit values of voltage and impedance are used internally for network calculations. It is assumed internally that the base power is 1 MW.

Note

For a full reference to the optimisation problem description, see https://pypsa.readthedocs.io/en/latest/optimal_power_flow.html

South Africa & Mozambique system example#

Compared to the previous example, we will consider a more complex system with more components (generators, transmission lines) and more buses. We also discuss basics of the plotting functionality built into PyPSA.

  • fuel costs in € / MWh\(_{th}\)

fuel_cost = dict(
    coal=8,
    gas=100,
    oil=48,
)

  • efficiencies of thermal power plants in MWh\(_{el}\) / MWh\(_{th}\)

efficiency = dict(
    coal=0.33,
    gas=0.58,
    oil=0.35,
)

  • specific emissions in t\(_{CO_2}\) / MWh\(_{th}\)

# t/MWh thermal
emissions = dict(
    coal=0.34,
    gas=0.2,
    oil=0.26,
    hydro=0,
    wind=0,
)

  • power plant capacities in MW

power_plants = {
    "SA": {"coal": 35000, "wind": 3000, "gas": 8000, "oil": 2000},
    "MZ": {"hydro": 1200},
}

  • electrical load in MW

loads = {
    "SA": 42000,
    "MZ": 650,
}

Building a basic network#

By convention, PyPSA is imported without an alias:

import pypsa

First, we create a new network object which serves as the overall container for all components.

n = pypsa.Network()

Let’s repeat: Buses are the fundamental nodes of the network, to which all other components like loads, generators and transmission lines attach. They enforce energy conservation for all elements feeding in and out of it (i.e. Kirchhoff’s Current Law).

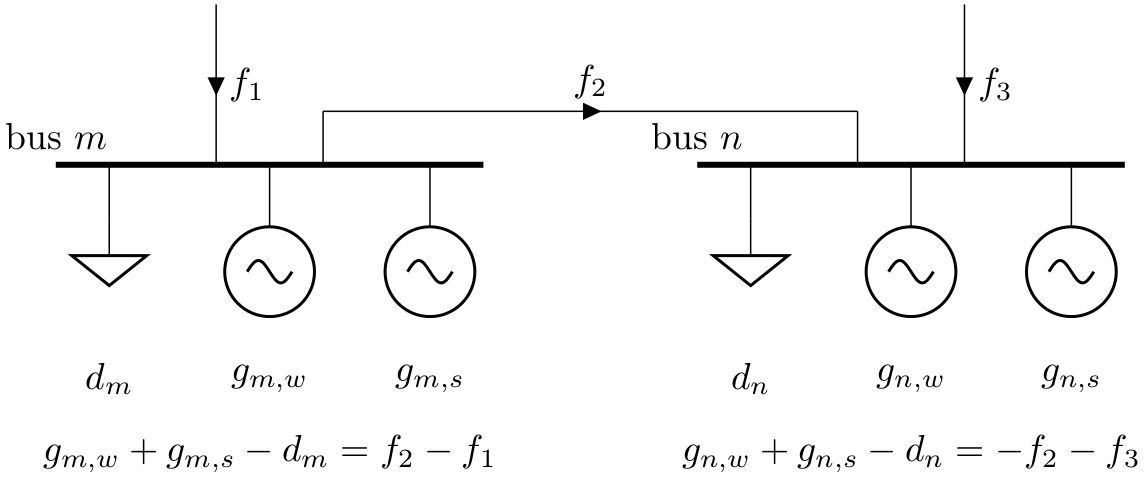
Components can be added to the network n using the n.add() function. It takes the component name as a first argument, the name of the component as a second argument and possibly further parameters as keyword arguments. Let’s use this function, to add buses for each country to our network:

n.add("Bus", "SA", y=-30.5, x=25, v_nom=380, carrier="AC")
n.add("Bus", "MZ", y=-18.5, x=35.5, v_nom=380, carrier="AC")

Index(['MZ'], dtype='object')

n.buses
v_nom type x y carrier unit v_mag_pu_set v_mag_pu_min v_mag_pu_max control generator sub_network
Bus
SA 380.0 25.0 -30.5 AC 1.0 0.0 inf PQ
MZ 380.0 35.5 -18.5 AC 1.0 0.0 inf PQ

You see there are many more attributes than we specified while adding the buses; many of them are filled with default parameters which were added. You can look up the field description, defaults and status (required input, optional input, output) for buses here https://pypsa.readthedocs.io/en/latest/components.html#bus, and analogous for all other components.

The method n.add() also allows you to add multiple components at once. For instance, multiple carriers for the fuels with information on specific carbon dioxide emissions, a nice name, and colors for plotting. For this, the function takes the component name as the first argument and then a list of component names and then optional arguments for the parameters. Here, scalar values, lists, dictionary or pandas.Series are allowed. The latter two needs keys or indices with the component names.

n.add(
    "Carrier",
    ["coal", "gas", "oil", "hydro", "wind"],
    co2_emissions=emissions,
    nice_name=["Coal", "Gas", "Oil", "Hydro", "Onshore Wind"],
    color=["grey", "indianred", "black", "aquamarine", "dodgerblue"],
)

n.add("Carrier", ["electricity", "AC"])

Index(['electricity', 'AC'], dtype='object')

n.carriers
co2_emissions color nice_name max_growth max_relative_growth
Carrier
coal 0.34 grey Coal inf 0.0
gas 0.20 indianred Gas inf 0.0
oil 0.26 black Oil inf 0.0
hydro 0.00 aquamarine Hydro inf 0.0
wind 0.00 dodgerblue Onshore Wind inf 0.0
electricity 0.00 inf 0.0
AC 0.00 inf 0.0

Let’s add a generator in Mozambique:

n.add(
    "Generator",
    "MZ hydro",
    bus="MZ",
    carrier="hydro",
    p_nom=1200,  # MW
    marginal_cost=0,  # default
)

Index(['MZ hydro'], dtype='object')

# check that the generator was added
n.generators
bus control type p_nom p_nom_mod p_nom_extendable p_nom_min p_nom_max p_min_pu p_max_pu ... min_up_time min_down_time up_time_before down_time_before ramp_limit_up ramp_limit_down ramp_limit_start_up ramp_limit_shut_down weight p_nom_opt
Generator
MZ hydro MZ PQ 1200.0 0.0 False 0.0 inf 0.0 1.0 ... 0 0 1 0 NaN NaN 1.0 1.0 1.0 0.0

1 rows × 37 columns

power_plants["SA"].items()

dict_items([('coal', 35000), ('wind', 3000), ('gas', 8000), ('oil', 2000)])

Add generators in South Africa (in a loop):

for tech, p_nom in power_plants["SA"].items():
    n.add(
        "Generator",
        f"SA {tech}",
        bus="SA",
        carrier=tech,
        efficiency=efficiency.get(tech, 1),
        p_nom=p_nom,
        marginal_cost=fuel_cost.get(tech, 0) / efficiency.get(tech, 1),
    )

The complete n.generators DataFrame looks like this now:

n.generators.T
Generator MZ hydro SA coal SA wind SA gas SA oil
bus MZ SA SA SA SA
control PQ PQ PQ PQ PQ
type
p_nom 1200.0 35000.0 3000.0 8000.0 2000.0
p_nom_mod 0.0 0.0 0.0 0.0 0.0
p_nom_extendable False False False False False
p_nom_min 0.0 0.0 0.0 0.0 0.0
p_nom_max inf inf inf inf inf
p_min_pu 0.0 0.0 0.0 0.0 0.0
p_max_pu 1.0 1.0 1.0 1.0 1.0
p_set 0.0 0.0 0.0 0.0 0.0
e_sum_min -inf -inf -inf -inf -inf
e_sum_max inf inf inf inf inf
q_set 0.0 0.0 0.0 0.0 0.0
sign 1.0 1.0 1.0 1.0 1.0
carrier hydro coal wind gas oil
marginal_cost 0.0 24.242424 0.0 172.413793 137.142857
marginal_cost_quadratic 0.0 0.0 0.0 0.0 0.0
active True True True True True
build_year 0 0 0 0 0
lifetime inf inf inf inf inf
capital_cost 0.0 0.0 0.0 0.0 0.0
efficiency 1.0 0.33 1.0 0.58 0.35
committable False False False False False
start_up_cost 0.0 0.0 0.0 0.0 0.0
shut_down_cost 0.0 0.0 0.0 0.0 0.0
stand_by_cost 0.0 0.0 0.0 0.0 0.0
min_up_time 0 0 0 0 0
min_down_time 0 0 0 0 0
up_time_before 1 1 1 1 1
down_time_before 0 0 0 0 0
ramp_limit_up NaN NaN NaN NaN NaN
ramp_limit_down NaN NaN NaN NaN NaN
ramp_limit_start_up 1.0 1.0 1.0 1.0 1.0
ramp_limit_shut_down 1.0 1.0 1.0 1.0 1.0
weight 1.0 1.0 1.0 1.0 1.0
p_nom_opt 0.0 0.0 0.0 0.0 0.0

Next, we’re going to add the electricity demand.

A positive value for p_set means consumption of power from the bus.

n.add(
    "Load",
    "SA electricity demand",
    bus="SA",
    p_set=loads["SA"],
    carrier="electricity",
)

n.add(
    "Load",
    "MZ electricity demand",
    bus="MZ",
    p_set=loads["MZ"],
    carrier="electricity",
)

Index(['MZ electricity demand'], dtype='object')

n.loads
bus carrier type p_set q_set sign active
Load
SA electricity demand SA electricity 42000.0 0.0 -1.0 True
MZ electricity demand MZ electricity 650.0 0.0 -1.0 True

Finally, we add the connection between Mozambique and South Africa with a 500 MW line:

n.add(
    "Line",
    "SA-MZ",
    bus0="SA",
    bus1="MZ",
    s_nom=500,
    x=1,
    r=1,
)

Index(['SA-MZ'], dtype='object')

n.lines
bus0 bus1 type x r g b s_nom s_nom_mod s_nom_extendable ... v_ang_min v_ang_max sub_network x_pu r_pu g_pu b_pu x_pu_eff r_pu_eff s_nom_opt
Line
SA-MZ SA MZ 1.0 1.0 0.0 0.0 500.0 0.0 False ... -inf inf 0.0 0.0 0.0 0.0 0.0 0.0 0.0

1 rows × 31 columns

Optimisation#

With all input data transferred into PyPSA’s data structure, we can now build and run the resulting optimisation problem. We can have a look at the optimisation problem that will be solved by PyPSA with the n.optimize.create_model() function. This function returns a linopy model object:

n.optimize.create_model()

Linopy LP model
===============

Variables:
----------
 * Generator-p (snapshot, Generator)
 * Line-s (snapshot, Line)

Constraints:
------------
 * Generator-fix-p-lower (snapshot, Generator-fix)
 * Generator-fix-p-upper (snapshot, Generator-fix)
 * Line-fix-s-lower (snapshot, Line-fix)
 * Line-fix-s-upper (snapshot, Line-fix)
 * Bus-nodal_balance (Bus, snapshot)

Status:
-------
initialized

In PyPSA, building, solving and retrieving results from the optimisation model is contained in a single function call n.optimize(). This function optimizes dispatch and investment decisions for least cost. The n.optimize() function can take a variety of arguments. The most relevant for the moment is the choice of the solver. We already know some solvers from the introduction to linopy (e.g. “highs” and “gurobi”). They need to be installed on your computer, to use them here!

n.optimize(solver_name="highs")
Hide code cell output 
INFO:linopy.model: Solve problem using Highs solver

INFO:linopy.io: Writing time: 0.02s

INFO:linopy.constants: Optimization successful: 
Status: ok
Termination condition: optimal
Solution: 6 primals, 14 duals
Objective: 1.38e+06
Solver model: available
Solver message: optimal

INFO:pypsa.optimization.optimize:The shadow-prices of the constraints Generator-fix-p-lower, Generator-fix-p-upper, Line-fix-s-lower, Line-fix-s-upper were not assigned to the network.

Running HiGHS 1.9.0 (git hash: fa40bdf): Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [1e+00, 1e+00]
  Cost   [2e+01, 2e+02]
  Bound  [0e+00, 0e+00]
  RHS    [5e+02, 4e+04]
Presolving model
1 rows, 2 cols, 2 nonzeros  0s
0 rows, 0 cols, 0 nonzeros  0s
Presolve : Reductions: rows 0(-14); columns 0(-6); elements 0(-19) - Reduced to empty
Solving the original LP from the solution after postsolve
Model name          : linopy-problem-c6s69ay2
Model status        : Optimal
Objective value     :  1.3813912524e+06
Relative P-D gap    :  0.0000000000e+00
HiGHS run time      :          0.00
Writing the solution to /tmp/linopy-solve-jk_9935l.sol

('ok', 'optimal')

Let’s have a look at the results.

Since the power flow and dispatch are generally time-varying quantities, these are stored in a different location than e.g. n.generators. They are stored in n.generators_t. Thus, to find out the dispatch of the generators, run

n.generators_t.p
Generator MZ hydro SA coal SA wind SA gas SA oil
snapshot
now 1150.0 35000.0 3000.0 1500.0 2000.0

or if you prefer it in relation to the generators nominal capacity

n.generators_t.p / n.generators.p_nom
Generator MZ hydro SA coal SA wind SA gas SA oil
snapshot
now 0.958333 1.0 1.0 0.1875 1.0

You see that the time index has the value ‘now’. This is the default index when no time series data has been specified and the network only covers a single state (e.g. a particular hour).

Similarly you will find the power flow in transmission lines at

n.lines_t.p0
Line SA-MZ
snapshot
now -500.0 
n.lines_t.p1
Line SA-MZ
snapshot
now 500.0

The p0 will tell you the flow from bus0 to bus1. p1 will tell you the flow from bus1 to bus0.

What about the shadow prices?

n.buses_t.marginal_price
Bus SA MZ
snapshot
now 172.413793 -0.0

Basic network plotting#

For plotting PyPSA network, we’re going to need the help of some friends:

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

PyPSA has a built-in plotting function based on matplotlib, ….

n.plot(margin=1, bus_sizes=1)

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/cartopy/mpl/feature_artist.py:144: UserWarning:

facecolor will have no effect as it has been defined as "never".

(<matplotlib.collections.PatchCollection at 0x7f39092b1940>,
 <matplotlib.collections.LineCollection at 0x7f39092b1df0>)

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/cartopy/io/__init__.py:241: DownloadWarning:

Downloading: https://naturalearth.s3.amazonaws.com/50m_cultural/ne_50m_admin_0_boundary_lines_land.zip

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/cartopy/io/__init__.py:241: DownloadWarning:

Downloading: https://naturalearth.s3.amazonaws.com/50m_physical/ne_50m_coastline.zip
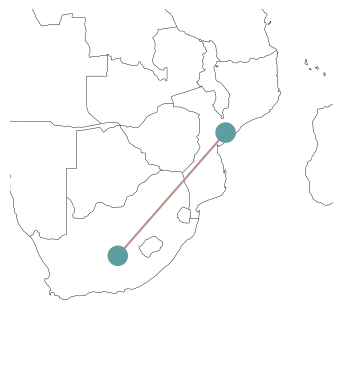
_images/c873b7ac8ae74c8bc4ef3cd2a2950947e8e09c55cb74b44c2f457d5be8e36c64.png

Since we have provided x and y coordinates for our buses, n.plot() will try to plot the network on a map by default. Of course, there’s an option to deactivate this behaviour:

n.plot(geomap=False)

(<matplotlib.collections.PatchCollection at 0x7f39091011f0>,
 <matplotlib.collections.LineCollection at 0x7f3909101190>)
_images/0bf2d37b4a5a4b5e5578146b538b4cb751590eec81f1e4b6b88d714704208c11.png

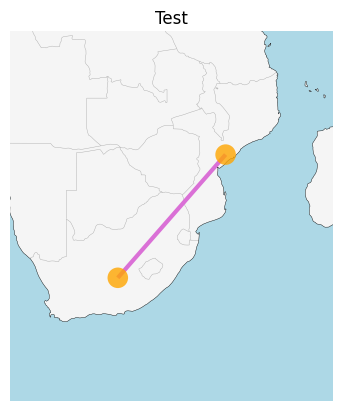
The n.plot() function has a variety of styling arguments to tweak the appearance of the buses, the lines and the map in the background:

n.plot(
    margin=1,
    bus_sizes=1,
    bus_colors="orange",
    bus_alpha=0.8,
    color_geomap=True,
    line_colors="orchid",
    line_widths=3,
    title="Test",
)

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/cartopy/mpl/feature_artist.py:144: UserWarning:

facecolor will have no effect as it has been defined as "never".

(<matplotlib.collections.PatchCollection at 0x7f390922bda0>,
 <matplotlib.collections.LineCollection at 0x7f3909099220>)

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/cartopy/io/__init__.py:241: DownloadWarning:

Downloading: https://naturalearth.s3.amazonaws.com/50m_physical/ne_50m_land.zip

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/cartopy/io/__init__.py:241: DownloadWarning:

Downloading: https://naturalearth.s3.amazonaws.com/50m_physical/ne_50m_ocean.zip
_images/c47f9e4e7f8326920a3078ec7577aa998b86b00d93402ee5b077f9ba91444789.png

We can use the bus_sizes argument of n.plot() to display the regional distribution of load. First, we calculate the total load per bus:

s = n.loads.groupby("bus").p_set.sum() / 1e4
s

bus
MZ    0.065
SA    4.200
Name: p_set, dtype: float64

The resulting pandas.Series we can pass to n.plot(bus_sizes=...):

n.plot(margin=1, bus_sizes=s)

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/cartopy/mpl/feature_artist.py:144: UserWarning:

facecolor will have no effect as it has been defined as "never".

(<matplotlib.collections.PatchCollection at 0x7f3909213c20>,
 <matplotlib.collections.LineCollection at 0x7f39092117c0>)
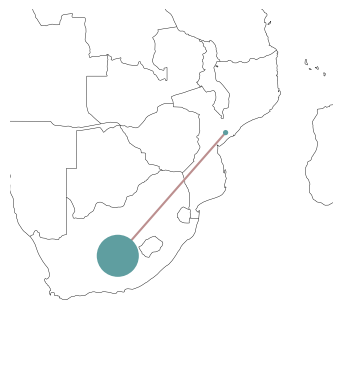
_images/0da186e3bad08bdd88761b6e95caae5ee9a3200eca986e357db8823e6ac6e20a.png

The important point here is, that s needs to have entries for all buses, i.e. its index needs to match n.buses.index.

The bus_sizes argument of n.plot() can be even more powerful. It can produce pie charts, e.g. for the mix of electricity generation at each bus.

The dispatch of each generator, we can find at:

n.generators_t.p.loc["now"]

Generator
MZ hydro     1150.0
SA coal     35000.0
SA wind      3000.0
SA gas       1500.0
SA oil       2000.0
Name: now, dtype: float64

If we group this by the bus and carrier…

n.generators.carrier

Generator
MZ hydro    hydro
SA coal      coal
SA wind      wind
SA gas        gas
SA oil        oil
Name: carrier, dtype: object

… we get a multi-indexed pandas.Series …

s = n.generators_t.p.loc["now"].groupby([n.generators.bus, n.generators.carrier]).sum()
s

bus  carrier
MZ   hydro       1150.0
SA   coal       35000.0
     gas         1500.0
     oil         2000.0
     wind        3000.0
Name: now, dtype: float64

… which we can pass to n.plot(bus_sizes=...):

n.plot(margin=1, bus_sizes=s / 3000)

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/cartopy/mpl/feature_artist.py:144: UserWarning:

facecolor will have no effect as it has been defined as "never".

(<matplotlib.collections.PatchCollection at 0x7f3933f5bf50>,
 <matplotlib.collections.LineCollection at 0x7f39092f3f80>)
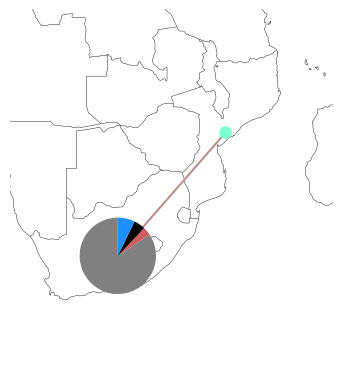
_images/d1ccfc3c1f1405e91bd8a8450e9992c3c225f2158a8a2db57da06fa2a58cbb06.png

How does this magic work? The plotting function will look up the colors specified in n.carriers for each carrier and match it with the second index-level of s.

Modifying networks#

Modifying data of components in an existing PyPSA network is as easy as modifying the entries of a pandas.DataFrame. For instance, if we want to reduce the cross-border transmission capacity between South Africa and Mozambique, we’d run:

n.lines.loc["SA-MZ", "s_nom"] = 100

n.lines
bus0 bus1 type x r g b s_nom s_nom_mod s_nom_extendable ... v_ang_max sub_network x_pu r_pu g_pu b_pu x_pu_eff r_pu_eff s_nom_opt v_nom
Line
SA-MZ SA MZ 1.0 1.0 0.0 0.0 100.0 0.0 False ... inf 0 0.000007 0.000007 0.0 0.0 0.000007 0.000007 500.0 380.0

1 rows × 32 columns

n.optimize(solver_name="highs")
Hide code cell output 
INFO:linopy.model: Solve problem using Highs solver

INFO:linopy.io: Writing time: 0.02s

INFO:linopy.constants: Optimization successful: 
Status: ok
Termination condition: optimal
Solution: 6 primals, 14 duals
Objective: 1.45e+06
Solver model: available
Solver message: optimal

INFO:pypsa.optimization.optimize:The shadow-prices of the constraints Generator-fix-p-lower, Generator-fix-p-upper, Line-fix-s-lower, Line-fix-s-upper were not assigned to the network.

Running HiGHS 1.9.0 (git hash: fa40bdf): Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [1e+00, 1e+00]
  Cost   [2e+01, 2e+02]
  Bound  [0e+00, 0e+00]
  RHS    [1e+02, 4e+04]
Presolving model
1 rows, 2 cols, 2 nonzeros  0s
0 rows, 0 cols, 0 nonzeros  0s
Presolve : Reductions: rows 0(-14); columns 0(-6); elements 0(-19) - Reduced to empty
Solving the original LP from the solution after postsolve
Model name          : linopy-problem-n9ad5cyb
Model status        : Optimal
Objective value     :  1.4503567697e+06
Relative P-D gap    :  3.2106671755e-16
HiGHS run time      :          0.00
Writing the solution to /tmp/linopy-solve-cr97nzzh.sol

('ok', 'optimal')

You can see that the production of the hydro power plant was reduced and that of the gas power plant increased owing to the reduced transmission capacity.

n.generators_t.p
Generator MZ hydro SA coal SA wind SA gas SA oil
snapshot
now 750.0 35000.0 3000.0 1900.0 2000.0

Add a global constraints for emission limits#

In the example above, we happen to have some spare gas capacity with lower carbon intensity than the coal and oil generators. We could use this to lower the emissions of the system, but it will be more expensive. We can implement the limit of carbon dioxide emissions as a constraint.

This is achieved in PyPSA through Global Constraints which add constraints that apply to many components at once.

But first, we need to calculate the current level of emissions to set a sensible limit.

We can compute the emissions per generator (in tonnes of CO\(_2\)) in the following way.

\[\frac{g_{i,s,t} \cdot \rho_{i,s}}{\eta_{i,s}}\]

where \( \rho\) is the specific emissions (tonnes/MWh thermal) and \(\eta\) is the conversion efficiency (MWh electric / MWh thermal) of the generator with dispatch \(g\) (MWh electric):

e = (
    n.generators_t.p
    / n.generators.efficiency
    * n.generators.carrier.map(n.carriers.co2_emissions)
)
e
Generator MZ hydro SA coal SA wind SA gas SA oil
snapshot
now 0.0 36060.606061 0.0 655.172414 1485.714286

Summed up, we get total emissions in tonnes:

e.sum().sum()

38201.49276011344

n.model

Linopy LP model
===============

Variables:
----------
 * Generator-p (snapshot, Generator)
 * Line-s (snapshot, Line)

Constraints:
------------
 * Generator-fix-p-lower (snapshot, Generator-fix)
 * Generator-fix-p-upper (snapshot, Generator-fix)
 * Line-fix-s-lower (snapshot, Line-fix)
 * Line-fix-s-upper (snapshot, Line-fix)
 * Bus-nodal_balance (Bus, snapshot)

Status:
-------
ok

So, let’s say we want to reduce emissions by 10%:

n.add(
    "GlobalConstraint",
    "emission_limit",
    carrier_attribute="co2_emissions",
    sense="<=",
    constant=e.sum().sum() * 0.9,
)

Index(['emission_limit'], dtype='object')

n.optimize.create_model()

Linopy LP model
===============

Variables:
----------
 * Generator-p (snapshot, Generator)
 * Line-s (snapshot, Line)

Constraints:
------------
 * Generator-fix-p-lower (snapshot, Generator-fix)
 * Generator-fix-p-upper (snapshot, Generator-fix)
 * Line-fix-s-lower (snapshot, Line-fix)
 * Line-fix-s-upper (snapshot, Line-fix)
 * Bus-nodal_balance (Bus, snapshot)
 * GlobalConstraint-emission_limit

Status:
-------
initialized

# let's check the new global constraint
n.model.constraints["GlobalConstraint-emission_limit"]

Constraint `GlobalConstraint-emission_limit`
--------------------------------------------
+1.03 Generator-p[now, SA coal] + 0.3448 Generator-p[now, SA gas] + 0.7429 Generator-p[now, SA oil] ≤ 34381.3434841021

n.optimize(solver_name="highs")
Hide code cell output 
INFO:linopy.model: Solve problem using Highs solver

INFO:linopy.io: Writing time: 0.02s

INFO:linopy.constants: Optimization successful: 
Status: ok
Termination condition: optimal
Solution: 6 primals, 15 duals
Objective: 2.21e+06
Solver model: available
Solver message: optimal

INFO:pypsa.optimization.optimize:The shadow-prices of the constraints Generator-fix-p-lower, Generator-fix-p-upper, Line-fix-s-lower, Line-fix-s-upper were not assigned to the network.

Running HiGHS 1.9.0 (git hash: fa40bdf): Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [3e-01, 1e+00]
  Cost   [2e+01, 2e+02]
  Bound  [0e+00, 0e+00]
  RHS    [1e+02, 4e+04]
Presolving model
2 rows, 3 cols, 6 nonzeros  0s
1 rows, 2 cols, 2 nonzeros  0s
0 rows, 0 cols, 0 nonzeros  0s
Presolve : Reductions: rows 0(-15); columns 0(-6); elements 0(-22) - Reduced to empty
Solving the original LP from the solution after postsolve
Model name          : linopy-problem-hf1m8_zw
Model status        : Optimal
Objective value     :  2.2123131990e+06
Relative P-D gap    :  6.3145844926e-16
HiGHS run time      :          0.00
Writing the solution to /tmp/linopy-solve-wzuyhsew.sol

('ok', 'optimal')

n.generators_t.p
Generator MZ hydro SA coal SA wind SA gas SA oil
snapshot
now 750.0 30156.761529 3000.0 8000.0 743.238471 
n.generators_t.p / n.generators.p_nom
Generator MZ hydro SA coal SA wind SA gas SA oil
snapshot
now 0.625 0.861622 1.0 1.0 0.371619 
n.global_constraints.mu

GlobalConstraint
emission_limit   -392.771084
Name: mu, dtype: float64

Can we lower emissions even further? Say by another 5% points?

n.global_constraints.loc["emission_limit", "constant"] = 0.85

n.optimize(solver_name="highs")
Hide code cell output 
INFO:linopy.model: Solve problem using Highs solver

INFO:linopy.io: Writing time: 0.02s

WARNING:linopy.constants:Optimization failed: 
Status: warning
Termination condition: infeasible
Solution: 0 primals, 0 duals
Objective: nan
Solver model: available
Solver message: infeasible

Running HiGHS 1.9.0 (git hash: fa40bdf): Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [3e-01, 1e+00]
  Cost   [2e+01, 2e+02]
  Bound  [0e+00, 0e+00]
  RHS    [8e-01, 4e+04]
Presolving model
Problem status detected on presolve: Infeasible
Model name          : linopy-problem-jpyv1stq
Model status        : Infeasible
Objective value     :  0.0000000000e+00
HiGHS run time      :          0.00
Writing the solution to /tmp/linopy-solve-51x6ppjb.sol

('warning', 'infeasible')

No! Without any additional capacities, we have exhausted our options to reduce CO2 in that hour. The optimiser tells us that the problem is infeasible.

A slightly more realistic example#

Dispatch problem with German SciGRID network

SciGRID is a project that provides an open reference model of the European transmission network. The network comprises time series for loads and the availability of renewable generation at an hourly resolution for January 1, 2011 as well as approximate generation capacities in 2014. This dataset is a little out of date and only intended to demonstrate the capabilities of PyPSA.

n = pypsa.examples.scigrid_de(from_master=True)

INFO:pypsa.examples:Retrieving network data from https://github.com/PyPSA/PyPSA/raw/master/examples/scigrid-de/scigrid-with-load-gen-trafos.nc

WARNING:pypsa.io:Importing network from PyPSA version v0.17.1 while current version is v0.32.1. Read the release notes at https://pypsa.readthedocs.io/en/latest/release_notes.html to prepare your network for import.

INFO:pypsa.io:Imported network scigrid-de.nc has buses, generators, lines, loads, storage_units, transformers

n.plot()

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/cartopy/mpl/feature_artist.py:144: UserWarning:

facecolor will have no effect as it has been defined as "never".

(<matplotlib.collections.PatchCollection at 0x7f3908dc0800>,
 <matplotlib.collections.LineCollection at 0x7f3908935970>,
 <matplotlib.collections.LineCollection at 0x7f3908700470>)
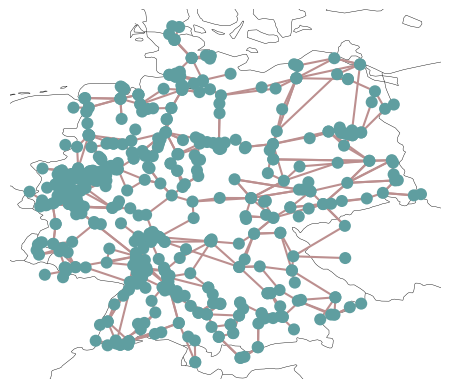
_images/c216de8d4fab4fc42a32aca240877e26da178753ea4b4009c070acd6ce9c0fbd.png

There are some infeasibilities without allowing extension. Moreover, to approximate so-called \(N-1\) security, we don’t allow any line to be loaded above 70% of their thermal rating. \(N-1\) security is a constraint that states that no single transmission line may be overloaded by the failure of another transmission line (e.g. through a tripped connection).

n.lines.s_max_pu = 0.7
n.lines.loc[["316", "527", "602"], "s_nom"] = 1715

Because this network includes time-varying data, now is the time to look at another attribute of n: n.snapshots. Snapshots is the PyPSA terminology for time steps. In most cases, they represent a particular hour. They can be a pandas.DatetimeIndex or any other list-like attributes.

n.snapshots

DatetimeIndex(['2011-01-01 00:00:00', '2011-01-01 01:00:00',
               '2011-01-01 02:00:00', '2011-01-01 03:00:00',
               '2011-01-01 04:00:00', '2011-01-01 05:00:00',
               '2011-01-01 06:00:00', '2011-01-01 07:00:00',
               '2011-01-01 08:00:00', '2011-01-01 09:00:00',
               '2011-01-01 10:00:00', '2011-01-01 11:00:00',
               '2011-01-01 12:00:00', '2011-01-01 13:00:00',
               '2011-01-01 14:00:00', '2011-01-01 15:00:00',
               '2011-01-01 16:00:00', '2011-01-01 17:00:00',
               '2011-01-01 18:00:00', '2011-01-01 19:00:00',
               '2011-01-01 20:00:00', '2011-01-01 21:00:00',
               '2011-01-01 22:00:00', '2011-01-01 23:00:00'],
              dtype='datetime64[ns]', name='snapshot', freq=None)

This index will match with any time-varying attributes of components:

n.loads_t.p_set["382_220kV"].plot(ylabel="MW")

<Axes: xlabel='snapshot', ylabel='MW'>
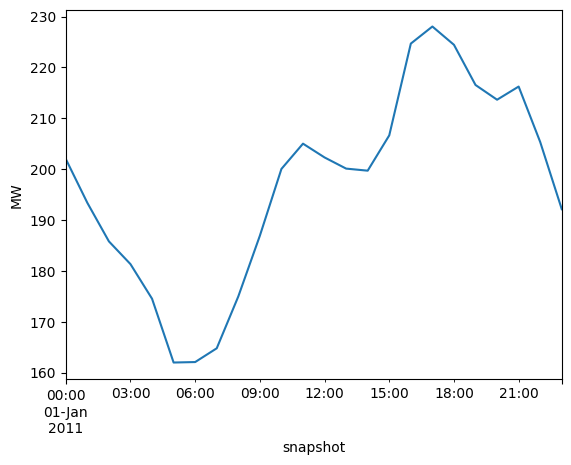
_images/cf1cc4e5c51f5572e3be80229e354fb9db5076118e9d2a0fc204fce092cadc79.png

Let’s inspect capacity factor time series for renewable generators:

n.generators_t.p_max_pu.T.groupby(n.generators.carrier).mean().T.plot(ylabel="p.u.")

<Axes: xlabel='snapshot', ylabel='p.u.'>
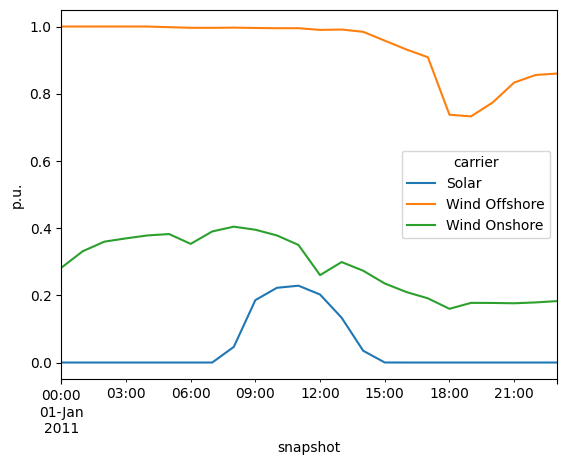
_images/759f36eb61e71f64fa5affafa98c74f136e63192dc2c1f59936a4556bd5a8ee6.png

We can also inspect the total power plant capacities per technology…

n.generators.carrier.unique()

array(['Gas', 'Hard Coal', 'Run of River', 'Waste', 'Brown Coal', 'Oil',
       'Storage Hydro', 'Other', 'Multiple', 'Nuclear', 'Geothermal',
       'Wind Offshore', 'Wind Onshore', 'Solar'], dtype=object)

n.generators.groupby("carrier").p_nom.sum().div(1e3).plot.barh()
plt.xlabel("GW")

Text(0.5, 0, 'GW')
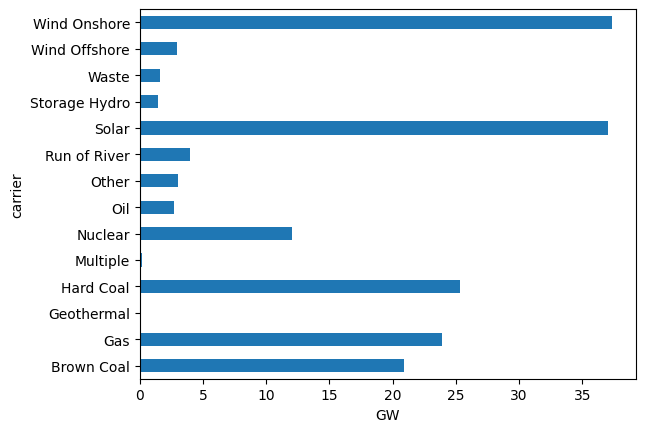
_images/6fb70f598b438c353d7ece1ca6e93451b1c59752bee4c29047722504b71f6c85.png

… and plot the regional distribution of loads…

load = n.loads_t.p_set.sum(axis=0).groupby(n.loads.bus).sum()

fig = plt.figure()
ax = plt.axes(projection=ccrs.EqualEarth())

n.plot(
    ax=ax,
    bus_sizes=load / 2e5,
)

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/cartopy/mpl/feature_artist.py:144: UserWarning:

facecolor will have no effect as it has been defined as "never".

(<matplotlib.collections.PatchCollection at 0x7f39087db2c0>,
 <matplotlib.collections.LineCollection at 0x7f39087dc560>,
 <matplotlib.collections.LineCollection at 0x7f3908ecfc20>)
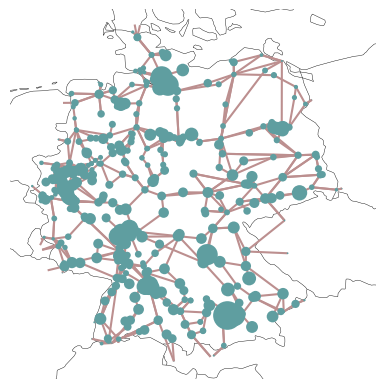
_images/0160d89f37a7a3c947efe46c61c2c86c26c8a5b8172e26bb24097b77ee715955.png

… and power plant capacities:

capacities = n.generators.groupby(["bus", "carrier"]).p_nom.sum()

For plotting we need to assign some colors to the technologies.

import random

carriers = list(n.generators.carrier.unique()) + list(n.storage_units.carrier.unique())
colors = ["#%06x" % random.randint(0, 0xFFFFFF) for _ in carriers]
n.add("Carrier", carriers, color=colors, overwrite=True)

Index(['Gas', 'Hard Coal', 'Run of River', 'Waste', 'Brown Coal', 'Oil',
       'Storage Hydro', 'Other', 'Multiple', 'Nuclear', 'Geothermal',
       'Wind Offshore', 'Wind Onshore', 'Solar', 'Pumped Hydro'],
      dtype='object')

Because we want to see which color represents which technology, we cann add a legend using the add_legend_patches function of PyPSA.

from pypsa.plot import add_legend_patches

fig = plt.figure()
ax = plt.axes(projection=ccrs.EqualEarth())

n.plot(
    ax=ax,
    bus_sizes=capacities / 2e4,
)

add_legend_patches(
    ax, colors, carriers, legend_kw=dict(frameon=False, bbox_to_anchor=(0, 1))
)

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/cartopy/mpl/feature_artist.py:144: UserWarning:

facecolor will have no effect as it has been defined as "never".
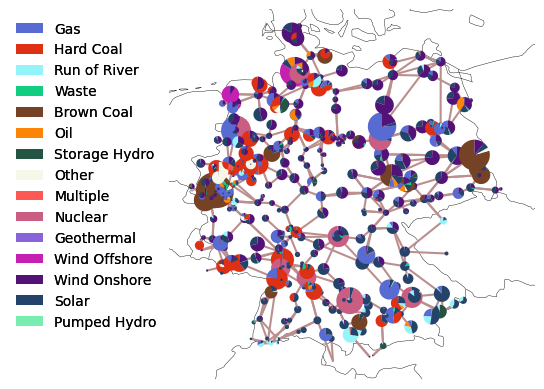
_images/5ad7cd00eb90532761066aa8e9fec11c8d18de707a3ac74bf0ac236a39a9cd66.png

This dataset also includes a few hydro storage units:

n.storage_units.head(3)
bus control type p_nom p_nom_mod p_nom_extendable p_nom_min p_nom_max p_min_pu p_max_pu ... state_of_charge_initial_per_period state_of_charge_set cyclic_state_of_charge cyclic_state_of_charge_per_period max_hours efficiency_store efficiency_dispatch standing_loss inflow p_nom_opt
StorageUnit
100_220kV Pumped Hydro 100_220kV PQ 144.5 0.0 False 0.0 inf -1.0 1.0 ... False NaN False True 6.0 0.95 0.95 0.0 0.0 0.0
114 Pumped Hydro 114 PQ 138.0 0.0 False 0.0 inf -1.0 1.0 ... False NaN False True 6.0 0.95 0.95 0.0 0.0 0.0
121 Pumped Hydro 121 PQ 238.0 0.0 False 0.0 inf -1.0 1.0 ... False NaN False True 6.0 0.95 0.95 0.0 0.0 0.0

3 rows × 33 columns

So let’s solve the electricity market simulation for January 1, 2011. It’ll take a short moment.

n.optimize(solver_name="highs")
Hide code cell output 
WARNING:pypsa.consistency:The following transformers have zero r, which could break the linear load flow:
Index(['2', '5', '10', '12', '13', '15', '18', '20', '22', '24', '26', '30',
       '32', '37', '42', '46', '52', '56', '61', '68', '69', '74', '78', '86',
       '87', '94', '95', '96', '99', '100', '104', '105', '106', '107', '117',
       '120', '123', '124', '125', '128', '129', '138', '143', '156', '157',
       '159', '160', '165', '184', '191', '195', '201', '220', '231', '232',
       '233', '236', '247', '248', '250', '251', '252', '261', '263', '264',
       '267', '272', '279', '281', '282', '292', '303', '307', '308', '312',
       '315', '317', '322', '332', '334', '336', '338', '351', '353', '360',
       '362', '382', '384', '385', '391', '403', '404', '413', '421', '450',
       '458'],
      dtype='object', name='Transformer')

WARNING:pypsa.consistency:The following transformers have zero r, which could break the linear load flow:
Index(['2', '5', '10', '12', '13', '15', '18', '20', '22', '24', '26', '30',
       '32', '37', '42', '46', '52', '56', '61', '68', '69', '74', '78', '86',
       '87', '94', '95', '96', '99', '100', '104', '105', '106', '107', '117',
       '120', '123', '124', '125', '128', '129', '138', '143', '156', '157',
       '159', '160', '165', '184', '191', '195', '201', '220', '231', '232',
       '233', '236', '247', '248', '250', '251', '252', '261', '263', '264',
       '267', '272', '279', '281', '282', '292', '303', '307', '308', '312',
       '315', '317', '322', '332', '334', '336', '338', '351', '353', '360',
       '362', '382', '384', '385', '391', '403', '404', '413', '421', '450',
       '458'],
      dtype='object', name='Transformer')

INFO:linopy.model: Solve problem using Highs solver

INFO:linopy.io:Writing objective.

Writing constraints.:   0%|          | 0/15 [00:00<?, ?it/s]

Writing constraints.:   7%|▋         | 1/15 [00:00<00:01,  9.01it/s]

Writing constraints.:  20%|██        | 3/15 [00:00<00:00, 12.10it/s]

Writing constraints.:  73%|███████▎  | 11/15 [00:00<00:00, 37.91it/s]

Writing constraints.: 100%|██████████| 15/15 [00:00<00:00, 22.89it/s]



Writing continuous variables.:   0%|          | 0/6 [00:00<?, ?it/s]

Writing continuous variables.:  50%|█████     | 3/6 [00:00<00:00, 29.76it/s]

Writing continuous variables.: 100%|██████████| 6/6 [00:00<00:00, 54.92it/s]

INFO:linopy.io: Writing time: 0.79s

Running HiGHS 1.9.0 (git hash: fa40bdf): Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
  Matrix [1e-02, 2e+02]
  Cost   [3e+00, 1e+02]
  Bound  [0e+00, 0e+00]
  RHS    [2e-11, 6e+03]
Presolving model
18737 rows, 44750 cols, 115742 nonzeros  0s
13266 rows, 39085 cols, 107646 nonzeros  0s

12708 rows, 31697 cols, 99739 nonzeros  0s
12699 rows, 31675 cols, 99730 nonzeros  0s
Presolve : Reductions: rows 12699(-130269); columns 31675(-27965); elements 99730(-163896)
Solving the presolved LP
Using EKK dual simplex solver - serial
  Iteration        Objective     Infeasibilities num(sum)
          0     0.0000000000e+00 Ph1: 0(0) 0s

      17203     9.1992880405e+06 Pr: 0(0); Du: 0(1.24345e-14) 4s
      17203     9.1992880405e+06 Pr: 0(0); Du: 0(1.24345e-14) 4s
Solving the original LP from the solution after postsolve
Model name          : linopy-problem-zceghxak
Model status        : Optimal
Simplex   iterations: 17203
Objective value     :  9.1992880405e+06
Relative P-D gap    :  1.5388259474e-14
HiGHS run time      :          4.43

INFO:linopy.constants: Optimization successful: 
Status: ok
Termination condition: optimal
Solution: 59640 primals, 142968 duals
Objective: 9.20e+06
Solver model: available
Solver message: optimal

INFO:pypsa.optimization.optimize:The shadow-prices of the constraints Generator-fix-p-lower, Generator-fix-p-upper, Line-fix-s-lower, Line-fix-s-upper, Transformer-fix-s-lower, Transformer-fix-s-upper, StorageUnit-fix-p_dispatch-lower, StorageUnit-fix-p_dispatch-upper, StorageUnit-fix-p_store-lower, StorageUnit-fix-p_store-upper, StorageUnit-fix-state_of_charge-lower, StorageUnit-fix-state_of_charge-upper, Kirchhoff-Voltage-Law, StorageUnit-energy_balance were not assigned to the network.

Writing the solution to /tmp/linopy-solve-yqeobjss.sol

('ok', 'optimal')

Now, we can also plot model outputs, like the calculated power flows on the network map.

n.lines.s_max_pu

Line
1      0.7
2      0.7
3      0.7
4      0.7
5      0.7
      ... 
855    0.7
856    0.7
857    0.7
858    0.7
859    0.7
Name: s_max_pu, Length: 852, dtype: float64

line_loading = n.lines_t.p0.iloc[0].abs() / n.lines.s_nom / n.lines.s_max_pu * 100  # %

norm = plt.Normalize(vmin=0, vmax=100)

fig = plt.figure(figsize=(7, 7))
ax = plt.axes(projection=ccrs.EqualEarth())

n.plot(
    ax=ax,
    bus_sizes=0,
    line_colors=line_loading,
    line_norm=norm,
    line_cmap="plasma",
    line_widths=n.lines.s_nom / 1000,
)

plt.colorbar(
    plt.cm.ScalarMappable(cmap="plasma", norm=norm),
    ax=ax,
    label="Relative line loading [%]",
    shrink=0.6,
)

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/cartopy/mpl/feature_artist.py:144: UserWarning:

facecolor will have no effect as it has been defined as "never".

<matplotlib.colorbar.Colorbar at 0x7f3900d008f0>
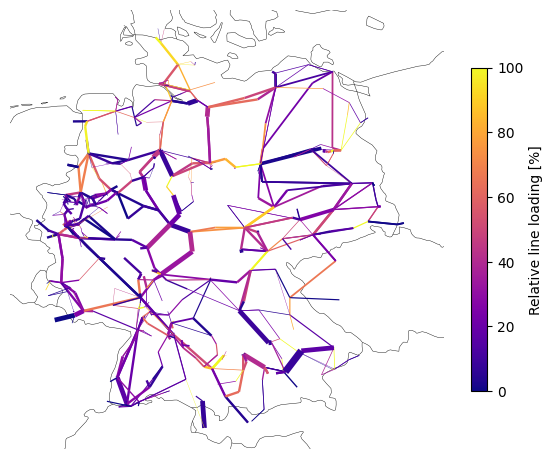
_images/47d510d513317bd2b39bdc02353f5db8548685de3d31c2b2f410f4dc5d6b63e8.png

Or plot the hourly dispatch grouped by carrier:

p_by_carrier = n.generators_t.p.T.groupby(n.generators.carrier).sum().T.div(1e3)

fig, ax = plt.subplots(figsize=(11, 4))

p_by_carrier.plot(
    kind="area",
    ax=ax,
    linewidth=0,
    cmap="tab20b",
)

ax.legend(ncol=5, loc="upper left", frameon=False)

ax.set_ylabel("GW")

ax.set_ylim(0, 80)

(0.0, 80.0)
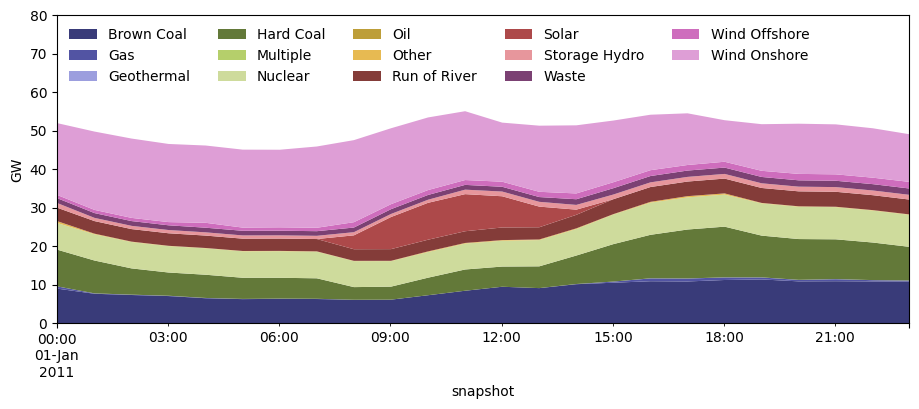
_images/26b8245013365fb652ac6752bc6b605b3c02f246bc02001c3ba5b8a6c34daa17.png

Or plot the locational marginal prices (LMPs):

fig = plt.figure(figsize=(7, 7))
ax = plt.axes(projection=ccrs.EqualEarth())

norm = plt.Normalize(vmin=0, vmax=100)  # €/MWh

n.plot(
    ax=ax,
    bus_colors=n.buses_t.marginal_price.mean(),
    bus_cmap="plasma",
    bus_norm=norm,
    bus_alpha=0.7,
)

plt.colorbar(
    plt.cm.ScalarMappable(cmap="plasma", norm=norm),
    ax=ax,
    label="LMP [€/MWh]",
    shrink=0.6,
)

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/cartopy/mpl/feature_artist.py:144: UserWarning:

facecolor will have no effect as it has been defined as "never".

<matplotlib.colorbar.Colorbar at 0x7f3908789c70>
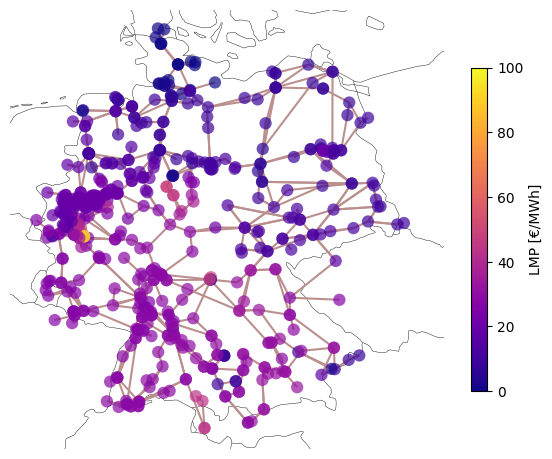
_images/b31156e5d67159bf244938f4ca4995de5cf680de6b45570b20677f79214c30a7.png

Data import and export#

Note

Documentation: https://pypsa.readthedocs.io/en/latest/import_export.html.

You may find yourself in a need to store PyPSA networks for later use. Or, maybe you want to import the genius PyPSA example that someone else uploaded to the web to explore.

PyPSA can be stored as netCDF (.nc) file or as a folder of CSV files.

  • netCDF files have the advantage that they take up less space than CSV files and are faster to load.

  • CSV might be easier to use with Excel.

n.export_to_csv_folder("tmp")

WARNING:pypsa.io:Directory tmp does not exist, creating it

INFO:pypsa.io:Exported network 'tmp' contains: lines, transformers, carriers, loads, generators, storage_units, buses

n_csv = pypsa.Network("tmp")

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/pypsa/io.py:159: UserWarning:

Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/pypsa/io.py:185: UserWarning:

Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/pypsa/io.py:185: UserWarning:

Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/pypsa/io.py:185: UserWarning:

Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/pypsa/io.py:185: UserWarning:

Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/pypsa/io.py:185: UserWarning:

Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/pypsa/io.py:185: UserWarning:

Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/pypsa/io.py:185: UserWarning:

Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/pypsa/io.py:185: UserWarning:

Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/pypsa/io.py:185: UserWarning:

Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/pypsa/io.py:185: UserWarning:

Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/pypsa/io.py:185: UserWarning:

Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/pypsa/io.py:185: UserWarning:

Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/pypsa/io.py:185: UserWarning:

Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/pypsa/io.py:185: UserWarning:

Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/pypsa/io.py:185: UserWarning:

Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.

INFO:pypsa.io:Imported network tmp has buses, carriers, generators, lines, loads, storage_units, transformers

n.export_to_netcdf("tmp.nc")

INFO:pypsa.io:Exported network 'tmp.nc' contains: lines, transformers, carriers, loads, generators, storage_units, buses

<xarray.Dataset> Size: 2MB
Dimensions:                            (snapshots: 24, investment_periods: 0,
                                        lines_i: 852, lines_t_p0_i: 852,
                                        lines_t_p1_i: 852, transformers_i: 96,
                                        transformers_t_p0_i: 96,
                                        transformers_t_p1_i: 96,
                                        carriers_i: 17, loads_i: 489,
                                        ...
                                        storage_units_t_p_dispatch_i: 30,
                                        storage_units_t_p_store_i: 30,
                                        storage_units_t_state_of_charge_i: 38,
                                        buses_i: 585, buses_t_p_i: 489,
                                        buses_t_v_ang_i: 585,
                                        buses_t_marginal_price_i: 584)
Coordinates: (12/24)
  * snapshots                          (snapshots) int64 192B 0 1 2 ... 21 22 23
  * investment_periods                 (investment_periods) int64 0B 
  * lines_i                            (lines_i) object 7kB '1' '2' ... '859'
  * lines_t_p0_i                       (lines_t_p0_i) object 7kB '1' ... '859'
  * lines_t_p1_i                       (lines_t_p1_i) object 7kB '1' ... '859'
  * transformers_i                     (transformers_i) object 768B '2' ... '...
    ...                                 ...
  * storage_units_t_p_store_i          (storage_units_t_p_store_i) object 240B ...
  * storage_units_t_state_of_charge_i  (storage_units_t_state_of_charge_i) object 304B ...
  * buses_i                            (buses_i) object 5kB '1' ... '458_220kV'
  * buses_t_p_i                        (buses_t_p_i) object 4kB '1' ... '458_...
  * buses_t_v_ang_i                    (buses_t_v_ang_i) object 5kB '1' ... '...
  * buses_t_marginal_price_i           (buses_t_marginal_price_i) object 5kB ...
Data variables: (12/84)
    snapshots_snapshot                 (snapshots) datetime64[ns] 192B 2011-0...
    snapshots_objective                (snapshots) float64 192B 1.0 1.0 ... 1.0
    snapshots_generators               (snapshots) float64 192B 1.0 1.0 ... 1.0
    snapshots_stores                   (snapshots) float64 192B 1.0 1.0 ... 1.0
    investment_periods_objective       (investment_periods) object 0B 
    investment_periods_years           (investment_periods) object 0B 
    ...                                 ...
    buses_ref                          (buses_i) object 5kB '' '' '' ... '' ''
    buses_osm_name                     (buses_i) object 5kB 'Hannover/West' ....
    buses_operator                     (buses_i) object 5kB 'TenneT;EON_Netz'...
    buses_t_p                          (snapshots, buses_t_p_i) float64 94kB ...
    buses_t_v_ang                      (snapshots, buses_t_v_ang_i) float64 112kB ...
    buses_t_marginal_price             (snapshots, buses_t_marginal_price_i) float64 112kB ...
Attributes:
    network__linearized_uc:      0
    network__multi_invest:       0
    network_name:                scigrid-de
    network_now:                 now
    network_objective:           9199288.04053981
    network_objective_constant:  0
    network_pypsa_version:       0.32.1
    network_srid:                4326
    crs:                         {"_crs": "GEOGCRS[\"WGS 84\",ENSEMBLE[\"Worl...
    meta:                        {}
n_nc = pypsa.Network("tmp.nc")

INFO:pypsa.io:Imported network tmp.nc has buses, carriers, generators, lines, loads, storage_units, transformers